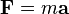Segunda ley

Segunda ley de Newton o Ley de fuerza

La segunda ley del movimiento de Newton dice que

El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.⁶

Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. En concreto, los cambios experimentados en el movimiento lineal de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; las fuerzas son causas que producen aceleraciones en los cuerpos. Consecuentemente, hay relación entre la causa y el efecto, la fuerza y la aceleración están relacionadas. Dicho sintéticamente, la fuerza se define simplemente en función del momento en que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.

En términos matemáticos esta ley se expresa mediante la relación:

Donde:

 es el momento lineal

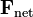 la fuerza total o fuerza resultante.

Suponiendo que la masa es constante y que la velocidad es muy inferior a la velocidad de la luz la ecuación anterior se puede reescribir de la siguiente manera:

Sabemos que  es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.

Consideramos a la masa constante y podemos escribir  aplicando estas modificaciones a la ecuación anterior:

La fuerza es el producto de la masa por la aceleracion, que es la ecuación fundamental de la dinámica, donde la constante de proporcionalidad, distinta para cada cuerpo, es su masa de inercia. Veamos lo siguiente, si despejamos m de la ecuación anterior obtenemos que m es la relación que existe entre  y . Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración (una gran masa) se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.

Por tanto, si la fuerza resultante que actúa sobre una partícula no es cero, esta partícula tendrá una aceleración proporcional a la magnitud de la resultante y en dirección de ésta. La expresión anterior así establecida es válida tanto para la mecanica clasica como para la mecanica relativista, a pesar de que la definición de momento lineal es diferente en las dos teorías: mientras que la dinámica clásica afirma que la masa de un cuerpo es siempre la misma, con independencia de la velocidad con la que se mueve, la mecánica relativista establece que la masa de un cuerpo aumenta al crecer la velocidad con la que se mueve dicho cuerpo.

De la ecuación fundamental se deriva también la definición de la unidad de fuerza o newton (N). Si la masa y la aceleración valen 1, la fuerza también valdrá 1; así, pues, el newton es la fuerza que aplicada a una masa de un kilogramo le produce una aceleración de 1 m/s². Se entiende que la aceleración y la fuerza han de tener la misma dirección y sentido.

La importancia de esa ecuación estriba sobre todo en que resuelve el problema de la dinámica de determinar la clase de fuerza que se necesita para producir los diferentes tipos de movimiento:rectilineo uniforme (m.r.u), circular uniforme (m.c.u) y uniformemente acelerado (m.r.u.a).

Si sobre el cuerpo actúan muchas fuerzas, habría que determinar primero el vector suma de todas esas fuerzas. Por último, si se tratase de un objeto que cayese hacia la tierra con una resistencia del aire igual a cero, la fuerza sería su peso, que provocaría una aceleración descendente igual a la de la gravedad.